树形振幅的简单解析
树形振幅 (Tree-level amplitudes)树形振幅的定义与意义在量子场论中,树形振幅是计算粒子间散射过程的关键概念。散射过程是描述粒子相互作用的一种手段,而散射振幅则是衡量这种相互作用强度的物理量。在微扰论框架内,我们可以通过计算 Feynman 图来求解散射振幅。其中,树形振幅是 Feynman 图中不包含闭合圈的图,具有最低阶的微扰贡献。 考虑一个 S 矩阵元素,表示从初始态进入散射过程,然后再从散射过程回到初始态的概率。这个过程可以用以下公式表示: S = 1 iT 其中,T 是传输矩阵元素,描述了粒子之间的相互作用过程。树形振幅正是这个传输矩阵元素的最低阶近似。 树形振幅在物理中的应用树形振幅在物理中的应用非常广泛,尤其是在粒子物理学和场论中。例如,在强子物理中,我们可以通过计算树形振幅来研究夸克和胶子之间的强相互作用。在弱相互作用中,树形振幅可以帮助我们理解 W 和 Z 玻色子与费米子之间的相互作用。此外,在电磁相互作用中,树形振幅也有重要应用,如计算光子与电子之间的散射过程。 黎曼曲面 (Riemann surfaces)黎曼曲面的基本概念黎曼曲面是一个复分析多样体,它具有局部性质和整体性质。局部性质指的是曲面上每个点都有一个邻域,这个邻域与复平面中的一个开集同胚。整体性质则反映了曲面的拓扑结构。在黎曼曲面上定义的复值函数被称为黎曼曲面上的全纯函数,它们在曲面的每个点都具有复解析性质。黎曼曲面的定义可用如下公式表示: 设$X$是一个连通的Hausdorff空间,若存在一族开集${U_i}$,使得$X = \bigcup_i U_i$,以及一族全纯映射${\phi_i: U_i \rightarrow \mathbb{C}}$,满足:
则称$(X, {U_i, \phi_i})$为一个黎曼曲面。 黎曼曲面的性质黎曼曲面的性质主要体现在它的全局性质和局部性质上。全局性质包括了黎曼曲面的拓扑不变量,如亏格(genus)和边界数(number of boundaries),以及黎曼曲面的基本群(fundamental group)。局部性质主要涉及到黎曼曲面上的全纯函数和正规族的性质。
黎曼映射定理的一个重要应用是在共形场论中,通过构造共形变换将复杂的几何结构化简为简单的几何结构,从而在较简单的几何背景下研究场的性质。 黎曼曲面在物理学中的应用弦论中的黎曼曲面在弦论中,弦在时空中的传播可以用黎曼曲面来描述。弦的世界面是一个二维曲面,它在弦论中的传播过程可以看作是黎曼曲面随着时间的演化。通过研究黎曼曲面的性质,可以得到弦的动力学行为和相互作用。例如,弦的散射振幅可以通过黎曼曲面上的Witten公式来计算,这个公式表达了黎曼曲面的拓扑不变量与弦散射振幅之间的关系。 共形场论中的黎曼曲面在共形场论中,黎曼曲面为研究共形不变性和Virasoro代数提供了理论基础。在共形场论中,物理量在共形变换下具有不变性,这意味着我们可以通过构造共形变换将复杂的几何结构化简为简单的几何结构。黎曼曲面在这个过程中发挥了重要作用,例如,我们可以使用黎曼映射定理来找到一个共形映射,将复杂的曲面映射到单位圆盘或整个复平面。 此外,黎曼曲面还在研究共形场论的基本对象(如基本场、顶点算符等)以及相应的代数结构(如Virasoro代数、Kac-Moody代数等)时发挥了重要作用。通过研究这些代数结构和黎曼曲面的性质,可以深入了解共形场论的动力学性质和关联函数。 二维量子引力中的黎曼曲面在二维量子引力研究中,黎曼曲面与拓扑及几何性质密切相关,为量子引力理论提供了重要的数学工具。在二维量子引力中,时空的几何结构被看作是一个黎曼曲面,研究其几何性质可以揭示量子引力的基本特征。例如,通过研究黎曼曲面的拓扑不变量,可以了解二维量子引力中的拓扑相变现象。此外,黎曼曲面上的共形不变性在二维量子引力中也起着重要作用,例如在李群和李代数的表示理论中,以及在研究二维量子引力的相互作用和相关性时。 标量期望值 (Scalar expectation values)在量子力学中,标量期望值是一个非常重要的概念,它可以帮助我们了解量子态的统计性质以及系统的平均行为。根据波恩规则,标量期望值可以表示为量子态与算符的内积。假设我们有一个量子态$|\psi\rangle$,以及一个描述物理量的算符$A$,那么物理量$A$在量子态$|\psi\rangle$下的期望值可以表示为: ⟨�⟩=⟨�∣�∣�⟩⟨ A ⟩=⟨ ψ ∣ A ∣ ψ ⟩ 其中,$\langle \psi|$表示$|\psi\rangle$的共轭转置。 在量子力学中,一个典型的例子是计算粒子在某个状态下的能量期望值。假设我们有一个单粒子的哈密顿量算符$\hat{H}$,那么能量期望值可以表示为: ⟨�⟩=⟨�∣�^∣�⟩⟨ E ⟩=⟨ ψ ∣ H ^∣ ψ ⟩ 这个期望值可以帮助我们了解粒子在这个状态下的平均能量。 不仅如此,标量期望值在量子力学中的应用还非常广泛,包括动量和位置等物理量的计算。例如,对于一个一维系统,位置算符为$\hat{x}$,动量算符为$\hat{p}$,那么位置期望值和动量期望值分别为: ⟨�⟩=⟨�∣�^∣�⟩⟨ x ⟩=⟨ ψ ∣ x ^∣ ψ ⟩ ⟨�⟩=⟨�∣�^∣�⟩⟨ p ⟩=⟨ ψ ∣ p ^∣ ψ ⟩ 在实际应用中,我们通常需要计算多个物理量的期望值,以便更全面地了解系统的行为。此外,标量期望值还在不确定性原理、波函数演化和量子测量等方面发挥着重要作用。例如,海森堡不确定性原理告诉我们,在同一时间内,粒子的位置$x$和动量$p$的不确定性不能同时达到最小值。这一原理可以通过计算位置和动量的期望值以及它们的方差来描述: Δ�Δ�≥ℏ2Δ x Δ p ≥2ℏ 其中,$\Delta x$和$\Delta p$分别表示位置和动量的标准差,$\hbar$是约化普朗克常数。 在场论中,标量期望值同样具有重要意义。在量子场论中,场算符描述了场的平均性质,例如标量场$\phi(x)$。场的期望值可以用来描述场的统计性质,例如计算场的关联函数。关联函数是一个描述场在不同空间点之间的关联性的重要量,它可以帮助我们了助我们了解场的波动和传播特性。对于标量场$\phi(x)$,其二点关联函数可以表示为: �(�,�)=⟨0∣�(�)�(�)∣0⟩ G ( x , y )=⟨0∣ ϕ ( x ) ϕ ( y )∣0⟩ 其中,$|0\rangle$表示真空态,$x$和$y$表示两个不同的时空点。通过计算关联函数,我们可以了解场在这两个点之间的相互作用特性。 在统计物理中,标量期望值也被用来计算响应函数。响应函数是一个描述系统在外部扰动下的响应特性的重要量,它可以帮助我们了解系统的平衡态和非平衡态性质。例如,在线性响应理论中,我们可以通过计算系统的线性响应函数来描述系统在外部场的作用下的响应。对于一个具有哈密顿量$H_0$的系统,假设我们施加了一个外部场$A$,那么系统的哈密顿量变为: �=�0 �� H = H 0 λA 其中,$\lambda$表示外部场的强度。在这种情况下,我们可以计算系统在外部场作用下的响应函数$R(t)$,它可以表示为: �(�)=�⟨�(�)⟩�� R ( t )= dλd ⟨ A ( t )⟩ 其中,$\langle A(t) \rangle$表示物理量$A$在时间$t$的期望值。通过计算响应函数,我们可以了解系统在外部扰动下的动力学行为和稳定性。 bc共形场论 (bc CFT)在讨论bc共形场论(bc CFT)之前,我们首先需要深入了解共形场论的基本概念。共形场论是一种具有共形不变性的场论,广泛应用于弦论、凝聚态物理和量子引力等领域。共形变换是一种保持角度不变的无穷小变换,因此,共形场论中的场在共形变换下具有不变性。在二维平面上,共形变换可以表示为: z' = f(z), 其中 z 和 z' 分别表示复平面上的原始点和变换后的点,而 f(z) 是一个解析函数。共形不变性限制了场的动力学行为,因此共形场论为研究场的关联函数和动力学行为提供了丰富的理论框架。 接下来,我们将详细讨论bc共形场论(bc CFT)的特点。在bc CFT中,场满足一定的边界条件,如狄利克雷或诺伊曼边界条件。这些边界条件限制了场的动力学行为,并使得bc共形场论成为理解带边界条件场系统的理论支持。例如,狄利克雷边界条件可以表示为: ϕ(x = 0) = 0, 诺伊曼边界条件则表示为: ∂ϕ(x = 0) / ∂x = 0, 其中 ϕ 是场, x 表示坐标。满足这些边界条件的场,在边界上会有特定的性质,如场值为零或场的导数为零。 在物理学中,bc共形场论有着广泛的应用。首先,在弦论中,bc CFT被用来描述开弦和闭弦之间的相互作用。开弦和闭弦是弦论中的基本对象,它们在时空中传播并相互作用。在描述这些相互作用时,我们需要考虑弦的边界条件,这就需要引入bc共形场论。例如,弦的边界条件可以表示为: ∂_τ X^μ(σ, τ) |_{σ=0} = 0,其中 X^μ 表示弦的坐标, σ 和 τ 是世界面坐标。通过求解满足这些边界条件的场方程,我们可以研究弦的散射过程和弦的边界态。 此外,在凝聚态物理中,bc CFT为研究二维临界现象和量子霍尔效应等问题提供了重要的理论框架。在二维临界临界现象中,共形场论可以用来描述关联长度发散的情况,通过计算关联函数和响应函数,我们可以研究临界点附近的物理性质。在这种情况下,bc共形场论可以用来考虑边界效应,例如,当研究界面上的临界现象时,边界条件就变得非常重要。同样,在量子霍尔效应中,电子在强磁场下的运动受到边界的影响,此时bc共形场论也可以发挥重要作用。 最后,bc共形场论还在量子引力和黑洞物理等领域发挥着重要作用。在量子引力中,我们需要考虑引力场的量子化,这就需要引入共形场论。在黑洞物理中,黑洞的熵和温度等热力学性质与共形场论密切相关,bc共形场论在这些问题中起到了关键作用。例如,在计算黑洞熵时,我们需要考虑黑洞的边界条件,这就涉及到bc共形场论。
结论本文简要介绍了树形振幅、黎曼曲面、标量期望值和bc共形场论这四个物理学概念。这些概念在物理学的不同领域中都有广泛的应用和重要的地位。通过深入理解这些概念,我们可以更好地掌握物理学的基本原理和方法,推动物理学的发展。 |
- 上一篇

什么是黑洞:数学黑洞、物理黑洞和天文黑洞
爱因斯坦在1905年提出了狭义相对论,把牛顿力学和麦克斯韦电磁学统一起来,给出了一个描述惯性系中物质和光线运动的新理论。但是狭义相对论有一个局限性,就是它不能处理加速系或者引力场中的情况。爱因斯坦又花了十年的时间,终于在1915年提出了广义相对论,把引力也纳入了相对论的框架,给出了一个描述时空和物质相互作用的新理论。数学黑洞爱因斯坦提出了广义相对论之后,很快就有人开始尝试寻找他的方程的解。
- 下一篇
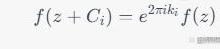
弦论中的S-矩阵解析
弦论中的S-矩阵弦论是一种试图解释宇宙中所有基本粒子和力的理论。而相互作用则通过弦之间的碰撞来描述。包括圆、环面、模空间和黎曼曲面,圆和环面的概念在平面解析几何中,圆的周长 L 和半径 r 之间存在以下关系:因为它揭示了弦振动周期与振幅之间的联系。基本粒子由弦的振动模式描述,R 是环面的主半径,可以得到不同形状的环面。环面在高维空间中描述弦的振动至关重要。

