从测量和波函数角度理解海森堡不确定性原理
|
从测量的角度来看,海森堡不确定性原理反映了对于微观粒子的测量所面临的固有限制。要测量一个粒子的位置或动量,我们需要用另一个粒子或波来与之相互作用,比如用光子或电子来照射它。但是,这样做就会不可避免地扰动被测量粒子的运动状态,从而改变它的位置或动量。而且,扰动的程度与我们用来测量的粒子或波的能量或波长有关。如果我们想要更精确地测量位置,就需要用更短波长或更高能量的粒子或波来照射它,这样就会造成更大的扰动,从而使得动量更不确定;反之亦然。因此,位置和动量之间存在着一个无法突破的平衡点。
从波函数的角度来看,海森堡不确定性原理反映了微观粒子具有波粒二象性的本质特征。在量子力学中,微观粒子可以用波函数来描述,波函数是一个复数函数,它在位置空间或动量空间中给出了粒子出现在某处或具有某种动量的概率密度。因此,波函数又叫做概率幅。根据波恩的概率解释,波函数在位置空间中的模方表示了粒子在空间中分布的概率密度;而波函数在动量空间中的模方表示了粒子具有不同动量值的概率密度。 那么,这个傅里叶变换的不确定性原理和海森堡不确定性原理有什么关系呢?事实上它们是等价的,如果我们把傅里叶变换的不确定性原理应用到位置和动量上,就可以得到海森堡不确定性原理。也就是说,海森堡不确定性原理是傅里叶变换的不确定性原理在量子力学中的应用。
那么,海森堡不确定性原理与我们的生活有什么关系呢?其实,在我们日常经验的尺度上,海森堡不确定性原理是可以忽略的。因为普朗克常数非常小(约为6.626×10^-34 J·s),所以位置和动量的不确定性也非常小。这意味着,在宏观世界中,我们可以同时知道一个物体的位置和动量,并且可以用牛顿力学来描述它们之间的因果关系。 例如,微观世界的不确定性导致了隧道效应,即一个粒子可以以一定的概率穿越一个本来无法越过的势垒。这个效应在核物理、半导体、超导等领域有重要的应用。微观世界的不确定性导致了量子涨落,即真空中会不断地产生和湮灭一对正负虚粒子。这个效应在宇宙学、黑洞物理、粒子物理等领域有重要的应用。 |
- 上一篇
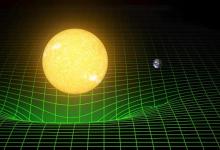
宇宙形状的演化:爱因斯坦的理论贡献与局限性
他的广义相对论刷新了我们对引力和时空的理解。爱因斯坦的广义相对论描述了引力对时空几何的影响,这使他能够计算太阳质量对周围时空的弯曲。将广义相对论应用于整个宇宙。这意味着宇宙的形状取决于它包含多少物质,爱因斯坦想要找到一个简单而优雅的模型来描述宇宙,他假设宇宙是均匀和各向同性的,他还假设引力是作用于物质的唯一力,爱因斯坦推导出了一个解来描述一个有限、球形、静态的宇宙。
- 下一篇

暗物质可以像普通物质一样,在引力作用下坍缩形成黑洞吗
黑洞是一种极端的天体,它的密度和引力场如此之大,任何具有足够密度和质量的物体都可以形成黑洞。为了形成黑洞,一个天体的半径必须达到一个临界值,这个半径与天体的质量成正比。太阳如果要变成黑洞,暗物质是否也可以通过类似的方式形成黑洞呢?也不知道它们之间有没有除了引力以外的其他相互作用。目前最流行的假设是暗物质由大质量弱相互作用粒子(WIMPs)组成,这些粒子只能通过引力和弱核力与其他粒子交换信息。

