宇宙形状的演化:爱因斯坦的理论贡献与局限性
|
爱因斯坦是有史以来最伟大的物理学家之一,他的广义相对论刷新了我们对引力和时空的理解。但他是如何设想宇宙的形状的呢?他做了哪些假设,又遇到了哪些挑战? 爱因斯坦的广义相对论描述了引力对时空几何的影响,这使他能够计算太阳质量对周围时空的弯曲。于是,在广义相对论发表后的两年,他又迈出了大胆的一步,将广义相对论应用于整个宇宙。这意味着宇宙的形状取决于它包含多少物质,以及物质如何分布。
爱因斯坦想要找到一个简单而优雅的模型来描述宇宙,使之与他的理论和观测一致。他假设宇宙是均匀和各向同性的,而且物质均匀地分布在整个空间中。当时,他还假设它是静态的,因为当时没有证据表明宇宙在膨胀。此外,他还假设引力是作用于物质的唯一力, 基于这些假设,爱因斯坦推导出了一个解来描述一个有限、球形、静态的宇宙。然而,爱因斯坦很快意识到他的模型存在问题,会造成宇宙不稳定。物质密度或压力稍微扰动会导致静态宇宙崩溃。为了防止发生这种情况,他在他的场方程中引入了一个新的术语:宇宙常数Λ。这个术语代表了一种排斥力,可以抵消引力的影响,使他的宇宙保持稳定。 爱因斯坦的静态宇宙是球形的,它的几何形状由一个参数决定:曲率,而宇宙的曲率又取决于物质。如果在给定半径范围内有太多的物质,空间就会是正弯曲的(就像一个球体)。如果在给定半径内物质太少,空间就会呈负弯曲(就像一个马鞍)。如果在给定半径内有足够的物质,空间就会是平的(就像一个平面)。爱因斯坦的静态宇宙似乎与当时可用的观测结果一致。
爱因斯坦的宇宙模型很快受到新理论和新观测的挑战。1922年至1924年,亚历山大·弗里德曼证明,爱因斯坦的方程除了静态解之外,还允许其他解的存在,即宇宙膨胀或收缩的解。1929-1931年间,埃德温·哈勃发现遥远的星系正以与其距离成正比的速度远离我们,这是宇宙膨胀的证据。这些进展使爱因斯坦相信他的静态模型是错误的,他在引入宇宙常数时犯了他一生中“最大的错误”。 1931年,乔治·勒梅特尔提出,如果将哈勃膨胀的时间倒退,那么宇宙会达到最初的高密度和高温度状态,也就是后来被称为大爆炸的状态。然而,爱因斯坦也从未完全接受大爆炸理论。 爱因斯坦的宇宙模型已经被现代宇宙学所取代,它基于广义相对论和大爆炸理论。现代宇宙学认为,宇宙在大尺度上仍然是均匀和各向同性的,但不是静态的,而是在膨胀的,这意味着任何两个足够远的点之间的距离随时间增加。
现代宇宙学也认为,宇宙的形状取决于其密度参数。根据最新观测数据,我们所处的可观测宇宙非常接近平坦。但这并不排除可观测区域外部或全局时空有其他形状或拓扑结构。 事实上,有一些理论家提出了一些更复杂或更奇特的模型来描述全局拓扑结构。例如,有人认为可观测区域可能只是一个巨大球面三维推广中很小部分,还有人认为可观测区域可能具有多重连通性(即存在“缝隙”或“捷径”),还有人认为可观测区域可能具有自相似性(即存在“分形”结构)。 这些模型都需要更多证据支持或否定。目前,我们还不能确定全局上真正形状或拓扑结构。但我们可以肯定一点:爱因斯坦给了我们一个启发性和创造性地思考问题方法。 |
- 上一篇

光速的测量:一个跨越千年的挑战
最早关于光速性质的思考可以追溯到古希腊时期。一种是亚里士多德等人认为光是无形无质无限快地传播的;另一种是恩培多克勒等人认为光是由微小粒子组成的,法国天文学家罗默首次利用天文现象成功地测出了光速。他发现木星卫星掩星发生时间与地球与木星距离有关:当地球靠近木星时掩星提前发生;当地球远离木星时掩星延后发生。罗默推断这是因为光需要花费一定时间从木星卫星传播到地球上观察者眼中所致。
- 下一篇
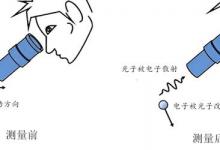
从测量和波函数角度理解海森堡不确定性原理
海森堡不确定性原理反映了对于微观粒子的测量所面临的固有限制。要测量一个粒子的位置或动量,这样做就会不可避免地扰动被测量粒子的运动状态,扰动的程度与我们用来测量的粒子或波的能量或波长有关。海森堡不确定性原理反映了微观粒子具有波粒二象性的本质特征。微观粒子可以用波函数来描述,它在位置空间或动量空间中给出了粒子出现在某处或具有某种动量的概率密度。

