诺特定理:对称性与守恒定律
|
那么,什么是对称性?举一个简单的例子,如果你将一个三角形旋转120度,它看起来是一样的。在诺特定理中,对称性更像是一个明确的数学问题。它表明,如果对等式进行更改,结果还是不变。例如,在方程y=x中,将每个x项都更改为负x,这个特定的等式不会改变。然后,我们就可以说方程在x与负x的变化下是对称的。
因此,这将我们带到了诺特定理。她证明的是,在物理系统中,某些对称性总是意味着守恒定律,而守恒定律总是意味着相应的对称性。 这三个熟悉的守恒定律源于我们方程的空间平移、时间平移和旋转平移属性的对称性。还有其他守恒定律则源于鲜为人知的特性。例如,电荷守恒定律源于量子力学方程中的某些对称性。
为什么诺特定理如此重要呢?这是因为她展示了守恒定律的来源:它们来自对称性。它甚至可能为我们未来的研究提供一些方向。不幸的是,诺特出生在一个没有完全欣赏她的世界。在女性机会有限的时代,她不被允许进入一些大学,即使她拥有一流的头脑。她作为教师时也没有得到相应的报酬,尽管得到了物理学和数学界一些知名人士的认可和支持,但她从未晋升为正教授。 艾米·诺特对人类知识的贡献非常多。她真的是个天才,对数学理论做出了许多贡献。但是,在物理学中,她以诺特定理而闻名:对于任何特定类别的对称性,都有一个守恒定律。她的定理与现代寻找新物理学有关。扩展我们目前对物理定律的理解的一种想法称为超对称,如果超对称是真实的,那么它应该有一个守恒量,发现守恒量是我们寻找超对称的方式之一。 |
- 上一篇
楼梯悖论:3 4=5的错误结论
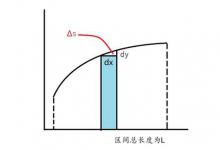
问题就在于,无限多个小误差累积起来会不会变成一个大误差。简单来说,积分求面积时的误差是两个无穷小长度的平方,即二阶无穷小。对它进行一阶无穷多次累加之后,我们得到的仍然是一阶无穷小。而对于所谓的楼梯悖论来说,它的误差是无穷小长度,即一阶无穷小,经过无穷多次累积后就可能变成一个可观的误差,所以折线不能用斜线代替。如果只是用上述的语言进行描述,那么有些人可能还有点怀疑。
- 下一篇

为什么1/137是物理学中未解决的问题之一
看起来就像为我们的物理定律提供动力的众多自然常数之一,它始于我们观察电子在原子能级之间跳跃时产生的光。这个过程导致发射特定能量的光子,解释谱线是量子力学发展的主要驱动力,首先是用玻尔模型解释氢线,然后是用薛定谔方程解释更重的元素。我们看到单条谱线实际上与计算值略有偏差,没有明显的理由表明这些不同的属性比率都应该是1/137或137的某个幂。

