望远镜的分辨率:波长与直径
|
过去的先贤已经总结了这个分离角以及观测时的光的波长还有望远镜直径之间的关系,可以用一条简单公式来描述这种关系:θ=kλ/D ,最小间隔角度 (θ) 等于一个常数乘以光的波长, 再除以望远镜直径。公式中的常数决定于能接受两个物体之间光照强度下降多少,一个广为接受的标准是瑞利极限。这个极限下,强度衰减约为26%。如果采用瑞利极限作标准, 常数K就等于1.22。我们尝试进行一个计算,如果望远镜直径 200mm,而且观测的是可见光谱, 波长就大概是0.5 μm,那么分离角大概是 3x10^-6 弧度,这真的非常小。
明白了这个理论,我们再来看看它的实际应用:接下来会比较几个星体在不同望远镜下的观测结果。第一台是1000mm直径的小观测站的望远镜,然后 200mm直径的业余爱好望远镜,第三个是24mm微型望远镜。它们都会看向距离2角秒的足够远的两个星体,1000mm望远镜下看起来就是两个小点,200mm望远镜也差不多,但是点变大了不少,最后24mm望远镜只能观测到一个模糊的大白点,根本没法看出来这其实是两颗星星。 为什么会出现这种现象?一个通常解释是光是一种波,以惠更斯-菲涅耳原理传播,就是解释衍射现象的那个原理。惠更斯原理指出,对于波的传播,波面上的每一点都是新的次级波面的波源。但惠更斯原理只描述了波的行为,却完全没有说明为什么会这样。 现在,如果我们用0.3mm直径的显微镜做个实验,我们会发现图像边缘有一圈圈涟漪,这是衍射所造成的。所有这些涟漪都会造成焦平面上清晰度的下降。
现在,詹姆斯·韦布望远镜成为了科学界焦点。它最大直径长达6.6m,比哈勃望远镜2.4米要大得多。但是有一点不同,韦布望远镜是分块的,每块之间的间隔比光的波长要大得多。刚开始我很担心这些间隔,因为每个间隔都会让能量向错误方向传播,,在波面上造成涟漪。但使用一些干涉特技, 很明显可以绕过这种现象,让分辨率仍然只决定于直径的总大小。综上,这让韦布望远镜的分辨率变成了哈勃的2.7倍。
韦伯望远镜分辨率的主要挑战其实还是在于它的目标光谱。再看一下上面分辨率的公式,波长也很重要。韦布望远镜将会观测红外光谱,也就是比可见光波长更长的光。由于宇宙膨胀,要想看得更远,所使用的波长就会越长。而根据公式,这会造成分辨率下降。 |
- 上一篇
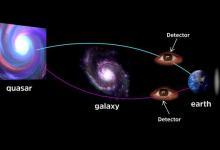
延迟选择量子擦除器:未来会影响现在吗?
可以通过两种不同的方式在地球上观察到这种光。因此在观察时它会被测量为光粒子。则来自这两个图像的组合光将被测量为波,并且测量的方式依赖于观测者的选择,这是否证明粒子对其当前状态的测量以某种方式影响了其过去的状态?解释量子理论的最传统方法是假设量子具有波函数,测量行为使量子粒子成为现实。因为光可能同时是波和粒子,采用标准双缝装置发射单光子,而是使用硼酸钡晶体将光子分成两个纠缠的光子。
- 下一篇
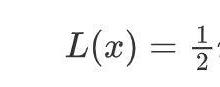
利用最小作用量原理,推导量子场论的基础方程
最小作用量原理是物理学中最基础的原理,我们利用最小作用量原理推导了广义相对论的运动方程,我们利用该原理来推导量子场论的基础方程——克莱因-戈登方程,它是薛定谔方程的狭义相对论形式,在推导该方程之前,我们先来简单的复习复习一下拉格朗日函数的推导过程。复习粒子从A点到B点的轨迹遵循最小作用量原理。在拉格朗日的方法中,动能减去势能为拉格朗日量,我们要找的是使作用量S最小的粒子的轨迹。

