诺贝尔物理学奖:康普顿效应
|
20世纪初是基础物理学领域空前进步的时期,其中大部分进展围绕着一个看似简单而无害的问题,即光的本质是什么以及它如何与物质相互作用。19世纪末电磁学的成功使许多人相信光是一种波,是电磁场中的一种自传播涟漪。 然而,爱因斯坦在1905年对光电效应的解释是基于这样一种观点,即光实际上是称为光子的粒子流,而不是连续变化的波。这些想法是基于马克斯·普朗克在1900年的开创性工作,他能够通过假设能量仅以离散的块或量子传输来解释热物体的辐射特性,而不是以经典物理学预测的连续方式。 尽管爱因斯坦的光子模型解释了光电效应,但许多物理学家仍然不愿意采用这种新的激进的光观点,毕竟除了光电效应,电磁学也是一个非常成功的理论,能够解释对自然界的极其广泛的观察。因此,物理学界要认真对待光子的想法,物理学家需要找到另一个例子,只能用光的光子模型进行解释。这需要一位对爱因斯坦和普朗克的工作表示赞赏的顶级实验物理学家。 康普顿散射1919年,亚瑟·康普顿在普林斯顿大学完成博士学位后,获得了国家研究委员会奖学金,使他能够在英国剑桥的卡文迪许实验室继续学习,康普顿正是在这里研究了伽马射线的散射和吸收。1922年,他完成了关于X 射线散射的开创性工作,一劳永逸地证实了光的光子理论。 康普顿的实验涉及将一束明确定义波长的X射线束引导到石墨靶上以进行各种散射角度,他测量了散射X射线的强度作为其波长的函数。康普顿发现,虽然入射光束由单一波长λ的X射线组成,但散射的X射线出现了两个波长峰值。其中一个峰值与入射波长λ相同,而另一个峰值λ'则大于λ,它们之间的差值Δλ=λ'-λ,也就是波长的康普顿位移。我们还可以从数据中看出,波长的康普顿位移随观察散射X射线的角度而增大。
那么根据电磁理论,我们如何理解这个实验结果?入射的X射线应该被视为电磁波,其频率对应于波的电场分量的振荡频率。入射X射线会导致石墨靶内的自由电子开始以与入射波相同的频率振荡。如果发射辐射的频率与入射辐射相同,经典电磁理论预测波长不应该有康普顿位移。 所以如何解释这个结果是关键,康普顿解释他的实验结果是使用光的光子模型。康普顿假设入射的X射线束由一束光子流组成,每个光子的能量为E=hf,并且这些光子与石墨中的自由电子发生一对一的碰撞,就像两个碰撞的台球一样。因为入射光子将其部分能量转移给与散射光子碰撞的电子,其能量就会低于入射光子。我们知道光子的能量与其频率成正比,也因为光速C=fλ,所以我们可以知道光子的能量与波长成反比。因此如果光子的能量减少,那么波长将增加,与观察到的实验结果就相符。 康普顿还注意到,散射辐射的波长与目标中包含的材料无关,这意味着散射过程确实 不涉及整个原子。康普顿因此假设散射是由于X射线光子与目标内部的单个电子之间的碰撞造成的,他还假设这些电子的行为就像它们完全自由一样。因此,康普顿能够使用动量守恒和能量守恒原理来提供电子-光子相互作用的详细计算,并预测散射光子波长的变化。 计算与解释结果引入直角坐标系,并将静止的电子定位在原点。我们将假设传入的X射线光子具有初始能量E_i和初始动量p_i,碰撞光子的能量E_f和动量p_f,并以相对于 X轴的角度θ的方向离开;而电子的动能是K动量是p,并以相对于X轴的角度φ的方向离开,如下图所示。
现在应用动量守恒:碰撞前的总动量必须等于碰撞后的总动量。沿X和Y方向的动量守恒公式分别如下:
如果我们将这两个表达式平方并将它们加在一起,通过一番求解我们可以得到以下等式:
接下来我们将能量守恒应用于粒子碰撞。能量守恒原理指出碰撞前的总能量必须等于碰撞后的总能量,于是我们有以下等式:
此外,爱因斯坦还给出了能量动量之间的关系:
其中,m_0是静止质量,而光子的静止质量为0,电子的静止质量为m_e,所以最终我们就可以得到两个等式:
现在,我们可以将所得到的结果放在一起,经过复杂的计算我们就可以得到:
为了得到波长之间的关系,我们给等式两边乘上普朗克常数h:、
然后,在利用等式λ=h/p,最终我们可以得到散射前后光子波长的关系:
从这个公式我们可以看出,波长的康普顿位移与散射角度相关联,可以解释实验所观察到的结果。康普顿相信理论和实验之间的这种显着一致性可以毫无疑问地证明X射线的散射是一种量子现象。康普顿效应和光子模型的解释在 1927年获得诺贝尔物理学奖。 |
- 上一篇
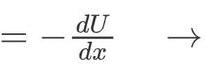
物理学中影响深远的思想之一:最小作用原理
假设我们有一个粒子,牛顿力学给了我们一种回答这个问题的方法,但是牛顿方法应用到向量,在18世纪拉格朗日和其他人提出了一个不同的建议,他们为每条可能的路径分配了一个称为作用量的数字,然后证明了粒子所遵循的轨迹实际上是作用量最小化的轨迹。我们应该写下粒子上的所有力,我们也知道了力是势能U的导数关系,在拉格朗日的方法中,其值为动能减去势能,粒子有非常多条可能的轨迹。
- 下一篇
“吃冰糖会触电”背后的物理
切割出一块石英晶体并压缩它,我们就能测量到切片上的电压,我们需要查看石英的晶格结构。起初石英的结构看起来非常复杂,但当我们旋转到合适的角度时,我们会发现熟悉的六边形形状。首先是晶格需要一些极性键,这意味着一些原子带有轻微的正电荷而另一些带有轻微的负电荷。它需要缺乏某种类型的对称性,否则压缩时电荷的平均位置不会改变,例如石英中六边形对角是不同种的原子。不能装上旋转风扇进行散热。

