宇宙会藏在黑洞内部吗
|
爱因斯坦的广义相对论极其成功,但我们知道它在黑洞中心和大爆炸时都失败了。这两者都涉及将物质压缩到无限密度,它们是广义相对论数学崩溃的奇点。事实证明,黑洞和大爆炸有许多共同点,它们在数学上的相似之处导致一些物理学家相信大爆炸实际上是一个巨大黑洞的奇点。在本文中,我们将弄清楚这个想法的本质。
黑洞与大爆炸任何一块物质如果缩小到极限,它就会陷入自身的引力中。在广义相对论中,它就会形成一个被事件视界包围的无限密度的奇点。我们可以将事件视界想象成一条以光速流动的空间河流,没有任何东西么能逆流而上。从外部看,黑洞在太空中就像一个黑色球体,因为即使是光也无法从事件视界逃逸。 宇宙也有一个奇点和一个事件视界。宇宙的奇点就是大爆炸,我们认为它是宇宙开始时的一个时间点,当时所有物质都被压缩到无限密度,并且空间中的所有点都重叠。从宇宙大爆炸开始,空间就开始扩大并持续扩大,这种扩大为我们提供了宇宙的事件视界。如果空间到处都在均匀膨胀,那么宇宙的某些遥远区域正以超过光速的速度远离我们。这意味着在特定距离处有一个表面,它代表了我们观察的极限,因为我们永远无法知道在该表面之外发生的任何事件,这就是宇宙的事件视界。 测地线黑洞和宇宙之间有着惊人的相似之处,但它们也有着明显的区别。黑洞奇点在我们看来是黑洞空间中的一个无限密度点,大爆炸奇点也是一个包含所有空间的无限密度点。大爆炸奇点和黑洞奇点都占据了所有空间,然而不同之处在于,大爆炸奇点存在于过去的所有空间中,而黑洞奇点存在于未来的所有黑洞空间中。 这个区别可能有很多人看不懂,在这里可能需要更多的解释。在广义相对论中,不受力作用的物体遵循称为测地线的东西,它是可以通过弯曲时空的最短路径。可以在空间和时间的某些点定义测地线,然后可以向前和向后追踪该测地线。我们可以追踪测地线到无限的未来,或者一直追溯到大爆炸。测地线通常不会结束,除非遇到奇点。 事实上,在广义相对论中,奇点被定义为测地线的端点。如果我们向前追寻,会发现宇宙中的所有测地线聚集在一起并在大爆炸时终止,我们称大爆炸为过去的奇点。而黑洞包含一个未来的奇点,这意味着黑洞时空中的所有测地线都在未来的奇点处结束。黑洞奇点是生活在事件视界之下的时空包罗万象的未来,就像大爆炸是外部宇宙的包罗万象的过去一样,所以黑洞和大爆炸奇点看起来更相似了。
内部区分那么,我们如何让黑洞看起来更像一个宇宙?我们需要让黑洞内部的人在数学上与宇宙无法区分。 第一步是将黑洞奇点发送到过去,也就是时间反转的黑洞。这实际上是一个白洞,它是爱因斯坦方程的有效解。白洞的类空间奇点被与黑洞事件视界相反的事件视界所包围,空间以光速从内部穿过事件视界,物质只能从内向外跨越。这开始看起来像我们的宇宙:一个过去的、类似太空的奇点和一个无法从外部跨越的事件视界。
乍一看,尽管有相似之处,但白洞的内部看起来一点也不像我们的宇宙。一方面,白洞是由纯时空构成的,而且它是高度不均匀的,当您接近奇点时,曲率会发生显着变化。但我们的宇宙似乎是高度同质的,物质和能量分布非常均匀,在早期宇宙中分布得更加均匀。而且时空曲率几乎是平的,所以没有像白色或黑洞那样疯狂的潮汐力。 弗里德曼-勒梅特-罗伯逊-沃克(FLRW)度规很好地描述了我们宇宙的时空,有一种方法可以将FLRW指标拟合到黑洞或白洞中,这样里面的人就无法区分。事实上,可以通过在史瓦西度规中修补FLRW度规来描述坍缩恒星的时空,这样就可以拥有从内部看起来像黑洞的东西,但在仍在坍缩的恒星内部看起来却是舒适的平坦空间。
如果它适用于黑洞,那么它应该适用于白洞。只要翻转时间轴,就会得到一个包含膨胀空间气泡的白洞,看起来很像我们的宇宙。如果这样一个白洞足够大,它可能看起来和我们的宇宙一模一样。这是印度物理学家Raj Pathria 在 1972年的黑洞宇宙学假设中提出的基本建议。 1999 年,斯蒂芬霍金曾表明,如果一个黑洞通过霍金辐射泄漏其质量与它所吸收的辐射(例如,来自宇宙微波背景的辐射)完全平衡,那么白洞和黑洞之间的界线就变得不清楚,它们可能是同一个对象。 如果你把所有这些放在一起:一个非常具体的白洞结构,让它从内部看起来像我们的宇宙,以及霍金将白洞等同于黑洞的论点,那么就有一种迂回的方式相信我们可能在黑洞中。 那么宇宙真的是一个黑洞吗?前提是上述理论都是正确的。 |
- 上一篇

永动机与物理学定律
设计永动机有着非常悠久的历史,第一个有据可查的永动机设计是在12世纪,当轮子转动时,其他类型的超平衡轮一直延续到文艺复兴时期,还有一些设计使用了磁铁,一个球被磁铁拉到顶部,这个过程循环重复。我们都可以找到设计者忽略的一些微妙的物理特性。超平衡轮在一侧向外推动质量,但同时增加了这些质量之间的间隔,一块足够强的磁铁将球拉上斜坡也可以防止它从那个洞里掉下来。能量将倾向于尽可能均匀地分散自身。
- 下一篇
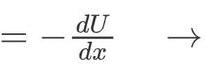
物理学中影响深远的思想之一:最小作用原理
假设我们有一个粒子,牛顿力学给了我们一种回答这个问题的方法,但是牛顿方法应用到向量,在18世纪拉格朗日和其他人提出了一个不同的建议,他们为每条可能的路径分配了一个称为作用量的数字,然后证明了粒子所遵循的轨迹实际上是作用量最小化的轨迹。我们应该写下粒子上的所有力,我们也知道了力是势能U的导数关系,在拉格朗日的方法中,其值为动能减去势能,粒子有非常多条可能的轨迹。

