如何从麦克斯韦方程组中得出光速
|
物体有一种叫做电荷的的属性 ,对于带负电荷的大型物体来说,这意味着它的电子比质子还多。如果我们有一个带电荷的静态物体,它只会影响其他电荷;如果我们有一个静态磁铁,它只会影响其他磁铁,而不会影响电荷。但如果我们有一个移动的电荷,它会影响磁铁;如果我们有一个移动的磁铁,则它会影响电荷。这就是这四个方程告诉我们的最简单的描述。
第一个方程称为高斯定律,它告诉我们电荷分布与电场的关系。其中ε是真空介电常数,它可以被认为是自由空间对电场形成的阻力。第二个方程被称为 高斯磁定律,它告诉我们通过任意封闭曲面的磁通量为零。第三个方程称为法拉第感应定律,它告诉我们变化的磁场会产生一个电场。第四个方程是麦克斯韦-安培定律,它告诉我们磁场可以由两种方法生成。等式右边第一项描述了第一种生成磁场的方法:电流,其中μ是真空磁导率,它被认为是自由空间允许磁力线穿透的能力。等式右边第二项描述了生成磁场的第二种方法:变化的电场,电场产生磁场的想法是麦克斯韦对安培定律的补充。 光速的推导而后,我们就可以把第四个方程代入式,得到:
真空中的麦克斯韦方程组中的第一个方程告诉我们,电场E的散度为零,因此我们就有:
我们知道一般的波动方程的形式如下:
所以光速公式所说的是这个波的速度与真空介电常数和真空磁导率有关,这有什么意义吗? 真空介电常数的数值为8.8542×10^-12,真空磁导率的数值是4π×10^-7。我们把这两个数值代入公式中,可以得到光速为299792252m/s。 |
- 上一篇
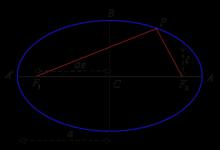
如何推导行星椭圆轨道方程
但该理论中行星是圆轨道,开普勒分析了他的老师第谷留下来的观测数据,开普勒是从实践中得出椭圆轨道,那么如何才能从理论上推导出椭圆轨道,椭圆的数学表达为了做到这一点。我们需要知道椭圆的数学表达式,我们都学过直角坐标系下的椭圆标准方程,偏心率e=c/a:在分析行星运动时,坐标原点取太阳中心比取椭圆中心更为自然, θ)代替直角坐标系(x,把它代入上述直角坐标系方程中:
- 下一篇

热力学:纯信息所消耗的能量
但计算机处理器不同,它的功能不是点亮、加热某物或四处移动。当我们要求它计算123乘以456时,我们并不期望得到任何有用的能量。我们想要的只是让它操纵信息,翻转一组0和1并给我们答案。那么这是否意味着处理器使用的能量都是耗散的能量呢?如果我们有一个能消除这些能量损失的办法,那么计算机处理器可以完全不用能量运行吗?答案是否定的,因为信息本身也有其自身的能源成本。

