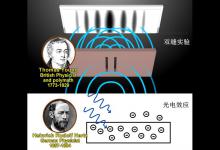
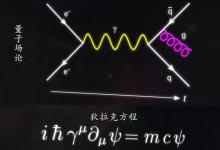
如果双缝实验扩展到无限个缝会发生什么？浅谈费曼路径积分

一个学生问：“如果在屏障上切第三条缝会发生什么？”显然，我们必须将穿过所有三个狭缝的波的振幅加在一起。那个学生继续问道：“但如果屏障上有四个、五个缝，甚至是无限的缝，连屏障都没有了，那应该怎么办呢？”没错，那个学生就是理查德·费曼，他刚刚概述了量子力学路径积分公式的基础知识。这是一个简单的想法，但它导致了有史以来最优雅的量子力学公式，并成为量子场论的关键。

最小作用原理

他的诀窍是将传播所花费的时间切成小间隔，并在每个时间步长上让粒子在空间中采取任何可以想象的直线步长。这给出了一组从起始点到终点的路径，其中一些看起来很正常，但大多数都是荒谬的。例如，有些路径会绕圈或绕道到达宇宙的边缘。

路径积分公式的惊人之处在于，费曼添加了一个且只有一个真实物理，那就是“最小作用原理”。它指出，一个对象将始终遵循作用量最小化的路径。这个作用量很难定义，它与路径上动能和势能之间的传递以及行程时间成正比。对于大尺度经典宇宙，最小化适当时间可以推导出几乎所有运动方程。然而，在量子宇宙中，没有单一的路径，费曼转而使用量子作用来为单个粒子可以采取的每条无限路径分配一个重要性——权重。然后，利用微积分的奇迹，他能够将所有这些无限可能路径的贡献加起来，以找到一个粒子从起点到终点进行简单旅行的概率。

现在，当费曼用这个作用量计算出他无限路径的概率幅值时，神奇的事情发生了。所有疯狂的路径都相互抵消，只有最明智的路径——那些作用量最少的路径，才显着增加了概率。大尺度经典世界中熟悉的路径只是不相互抵消的一小部分无限可能路径。

费曼的路径积分公式使他能够从零开始推导出薛定谔方程。路径积分方法在数学上等同于量子力学的早期推导，而且比量子力学的早期推导更强大。这种力量来自最小作用原理，该作用量是穿过时空的粒子路径的函数。这意味着它对称地对待空间和时间，因此与爱因斯坦的狭义相对论相匹配。