狄拉克方程:量子相对论与反物质的预测
|
到1920年代后期,爱因斯坦和普朗克已经证明光既是粒子也是波。德布罗意也从理论上证明所有物质都具有这种双重波粒性质。玻尔、海森堡、玻恩、泡利和其他人拼凑出对亚原子粒子怪异性质的数学描述。然后,在1926年,薛定谔写下了他著名的方程——薛定谔方程。它描述了这些表示波函数的物质波如何随时间变化,并使物理学家能够预测量子系统的演化。
然而,薛定谔方程也有问题。首先最明显的是,薛定谔方程与爱因斯坦的相对论完全不相容。在相对论中,空间和时间的维度本质上是相互联系的,它们随着参考系的变化而相互变动,但是薛定谔方程还是处于空间和时间相互独立的状态。相对论告诉我们,时间的流逝取决于速度,所以薛定谔方程只适用于缓慢移动的物体,但亚原子粒子通常以接近光速的速度移动。 英国物理学家保罗·狄拉克也考虑了这些问题,他想要一个适用于电子的薛定谔方程的完全相对论版本。他写下了爱因斯坦著名的方程:E=Mc,但其完整形式包括动量。然后,他使用量子力学表达式来表示能量和动量的关系。但最后的结果是一团糟。 狄拉克想出了一个称为“狄拉克海”的办法来解释这一点。想象一下宇宙中无处不在的电子海洋,这些电子占据所有负能量状态。只有当一个电子具有正能量时,我们才能真正与电子相互作用,而这个电子会浮在“海面”。如果这个想象中的海洋的能量状态都完全充满,那么额外的一个电子就不能再失去任何能量了。
狄拉克海的想法导致了奇怪的预测。从海面去除一个电子,它会留下一个空穴,这个空穴本身应该就像一个粒子。它会有惯性,就像它拥有丢失电子的质量一样;它也会表现得好像它具有与电子相反的电荷——正电荷。如果一个正能量电子发现其中一个空穴,它就会落入其中,这导致两者都被消灭,并释放出它们质量中的所有能量。
狄拉克在结合量子力学和狭义相对论方面的惊人洞察力揭示了我们宇宙的另一面——对反物质的预测,它也是发现量子场和量子场论以及发展粒子物理学标准模型的关键一步。 |
- 上一篇
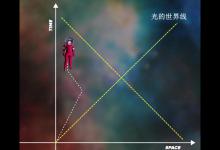
安鲁效应:从狭义相对论时空图说起
有质量的物体永远无法到达光速,因此包括观察者在内的任何有质量物体的世界线与垂直线的夹角必须小于45度。从我们的观察者向后延伸光线世界线定义了所谓的过去光锥,这是因为从过去光锥中的任何地方发射的光子可以到达我们的观察者。那么它的过去光锥最终应该包含整个宇宙(忽略宇宙膨胀)。那么在最接近的时候物体A发射的一个光子就永远赶不上观察者。远离黑洞的惯性观察者会看到辐射。
- 下一篇
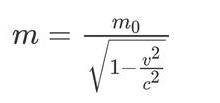
用两种方法推导爱因斯坦的质能方程
我们也用两种方法来推导质能方程。质量的相对论公式为:利用泰勒展开公式把右边项展开,右边第二项就是牛顿中的动能方程。为了解释上边式子的物理意义,爱因斯坦首先提出假设,物体的总能量等于质量与光速平方的乘积,上面的式子就是著名的爱因斯坦质能关系的公式。其中mc是物体的静能,第二种方法我们还可以用第二种方法来理解爱因斯坦的质能方程。动能定理仍然成立,但动能的形式有所不同。它做的功等于动能的变化。

