在黑洞中为何时间变成了空间,而空间变成了时间?
|
对于闵科夫斯基时空,这个量的定义如上图。不同的观察者可能会报告两个事件被不同的距离和时间分开:Δx和Δt。但是,所有观察者都记录相同的时间间隔。如果一个事件导致另一个事件,则时空间隔必须为零或者负数,这只是意味着它们之间可能存在因果关系。我们可以说一个物体在一个给定的时空瞬间是由它自己在更早的瞬间存在的,所以物体的世界线具有递减的时空间隔。事实上,前向事件演化需要负时空间隔。在平坦的时空中,Δt前面的符号推动了向前的演化,这使得t是类时间坐标,而x是类空间坐标。为了保持因果关系,类时间坐标必须始终增加。 下图是史瓦西对爱因斯坦方程的解(遗漏一些项),也是对黑洞的第一个准确描述。这个方程假设没有轨道运动,只有朝向或远离黑洞中心的运动,离中心的距离为r,而rs是史瓦西半径——事件视界的半径。
离事件视界很远的史瓦西时空会退化成平坦的闵科夫斯基时空,但是如果一个物体靠近事件视界,时空就会出现极度弯曲。但只要还在视界之外,时空间隔仍然是负的。但是一旦进入了视界之内,r就比rs还要小,此时这两个括号都变为负数:整个Δr变成是负的,而Δt则变成了正的。 在数学中,曾经代表距离的坐标r现在赋予了维持因果关系所需的负号,它变得像时间一样,它是单向的。与此同时,以前称为时间的坐标t失去了负号,变得跟空间一样,所以它可以向任何方向遍历。 |
- 上一篇
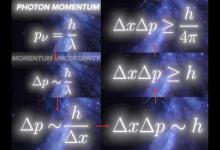
普朗克长度为什么是有意义的最小长度?
假设我们要测量到某个物体的距离,但是该距离测量具有不确定性,都会产生大约一个波长的距离不确定性。我们只需要使用非常短的波长就可以获得更高的测量精度。因此我们可以将光子的动量替换为被测物体的动量不确定性,并将波长替换为被测物体的位置不确定性,空间弯曲的位置不确定性假设我们正试图以完美的精度测量我们的距离,我们不断减少测量光子的波长,由此产生的引力场改变了到物体的距离。
- 下一篇

用几何描绘物理学的统一理论:卡鲁扎-克莱因理论
抽象的数学概念往往对物理学有用。这些高维几何对物理学家来说真的很方便,因为在物理学中,我们通常不仅要处理位于特定位置的事物,还要处理也会沿特定方向移动的事物。如果我们有一个粒子要描述它的作用,我们分别需要位置和动量的三维信息,因此实际上每个粒子都由一个六维空间中的向量来描述。这个六维空间称为相空间,通过处理相空间,物理学家变得习惯于处理更高维度的几何形状。自然而然。

