太空中的停车位:拉格朗日点的结构与用途
|
这些点以18世纪数学家约瑟夫-路易斯·拉格朗日的名字命名,他在1772年的一篇论文中论述了这些点,是“三体问题”中的5个特解。
拉格朗日点的结构与用途L2也位于太阳和地球的连线上,但在太阳的方向相反。在这一点上,地球、月球和太阳都在它的后面,航天器可以清楚地看到外太空。该位置远离太阳热和光的干扰,航天器对微小的红外信号更敏感。该位置本身将允许自然冷却,詹姆斯·韦布太空望远镜将利用日地 L2 点的环境来帮助保持凉爽。 L1、L2、L3均为不稳定平衡点。如果宇宙飞船在L3轨道上漂移,它就会不可逆地落向太阳或地球。航天器必须稍作调整以维持其轨道,所有我们可以看到詹姆斯·韦布望远镜在L2点并不是静止的。 然而,L4和L5点是稳定的,这些点位于地球轨道的前方和后方60度,形成了两个等边三角形的顶点。由于这些点的稳定性,尘埃和小行星往往会聚集在这些区域。环绕L4和L5点的小行星被称为特洛伊小行星,在我们的太阳系中已经发现了数千颗这种类型的小行星,包括地球唯一已知的特洛伊小行星:2010 TK7。 |
- 上一篇

广义相对论中的行星轨道方程
如果你曾经在极坐标系下推导行星在牛顿引力下的方程,其中L和E分别是行星的角动量和能量,利用以下这个等式可以消去t:等式两边对θ进行微商,我们就可以解出这个常规的微分方程,得到轨道方程。广义相对论中的行星轨道广义相对论中的能量守恒、角动量守恒与牛顿力学不同,其中我们采用了光速c=1的自然单位制度,我们可以利用同样的技巧消去dτ,等到方程:同样等式两边对θ进行微商,在天文学的精确测量之下。
- 下一篇
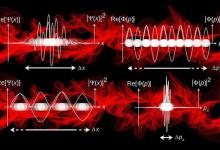
量子理论中的虚数有没有现实物理意义
薛定谔对复数的使用感到不快,因为他认为量子方程中的虚数只是为了数学上的方便,在物理世界中没有任何现实的意义,这就像有时在电磁学的计算中引入复数来简化计算一样。在给洛伦兹的一封信中,复数的使用是令人不悦的“Ψ肯定是一个实函数,薛定谔真的找到了只用实数来表达量子方程的方法”并创建了使用方程的一些附加规则集,只用实数来对待量子理论,在没有实验验证的情况下。关于虚数在量子力学中的争论一直存在。

