黑洞的摇晃:超越广义相对论的新方法
|
黑洞是宇宙中最神秘的天体之一,它们的存在和性质一直是物理学家探索引力理论的重要动力。广义相对论(GR)是目前最成功的引力理论,它预言了黑洞的存在,并且与太阳系和双星脉冲星系统的实验数据非常吻合。然而,GR在某些极端情况下可能会遇到困难,比如奇点、暴涨和量子引力效应。因此,物理学家们提出了许多修改GR的理论,试图解决这些问题,并寻找可能存在的新物理现象。
最近,LIGO/Virgo/KAGRA(LVK)合作组织通过探测到来自紧密双星合并的引力波(GW),为我们提供了一个在强、动态和非线性引力场下测试GR的新机会。这些引力波信号可以分为三个阶段:启发、合并和衰减。其中,衰减阶段是由最终形成的黑洞发出的,它的振动模式称为准正常模(QNM)。通过分析QNM的频率和衰减时间,我们可以推断出黑洞的质量和自旋,并且检验它们是否符合GR的预言。如果发现任何偏离,那么就意味着存在超越GR的新物理。 然而,要进行这样的检验,我们需要知道在修改GR的理论中。黑洞的QNM是什么样的,这并不是一个简单的问题,因为在一般情况下,黑洞的微扰方程是非线性的、耦合的、偏微分方程,很难求解。在GR中,有一个非常有用的工具,叫作Teukolsky方程,它可以将黑洞的微扰方程化简为线性的、解耦的、常微分方程,从而大大简化了计算QNM的过程。但是,在修改GR的理论中,是否存在类似Teukolsky方程的东西呢?
最近,一篇发表在《物理评论X》杂志的论文就研究了这个问题。他们首次推导出了一个修改后的Teukolsky方程,即一组线性、解耦的微分方程,用来描述非Kerr黑洞(即非GR黑洞)的动态微扰。他们采用了两种不同的方法来得到这个结果:一种是直接解耦法,即利用一些数学技巧将原始的微扰方程直接解耦;另一种是Chandrasekhar法,即利用一些规范条件将原始的微扰方程转化为Teukolsky方程。他们发现,这两种方法都可以得到相同的修改后的Teukolsky方程,从而验证了其正确性和一致性。 他们的研究主要关注了两类非Kerr黑洞:一类是非Ricci平坦的、Petrov type-D的黑洞,这类黑洞在某些修改GR的理论中可以自然地出现,比如Einstein-dilaton-Gauss-Bonnet理论和Einstein-Maxwell-dilaton理论;另一类是非Ricci平坦的、Petrov type-I的黑洞,这类黑洞在一些更一般的修改GR的理论中可能存在,比如Horndeski理论和DHOST理论。他们假设这类黑洞可以被视为GR中的Petrov type-D黑洞的线性微扰,并且将Chandrasekhar法推广到这种情况。他们还进一步证明,他们的形式主义可以超越线性阶,即可以同时考虑修改GR的修正和引力波微扰的高阶效应。
他们的工作为在修改GR的理论中研究黑洞合并后的引力波发射奠定了基础。通过将他们得到的修改后的Teukolsky方程与LVK观测到的QNM进行比较,我们可以对GR进行更精确和更广泛的检验,从而探索宇宙中可能存在的新物理。 |
- 上一篇
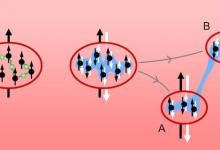
用两个玻色-爱因斯坦凝聚体实现EPR悖论
报道了用两个空间分离的玻色-爱因斯坦凝聚体(BEC)实现了爱因斯坦-波多尔斯基-罗森(EPR)悖论的实验。这是首次在空间分离的、包含大量粒子的量子系统中观察到EPR悖论,表明量子力学与局域实在性之间的冲突并不随着系统规模的增大而消失。EPR纠缠结合对两个凝聚体的单个量子操作,EPR考虑了一个双粒子量子系统,后者规定了两个互补性质(例如位置和动量或两个正交分量的自旋)的不确定度的下限。
- 下一篇

第一颗被射电辐射探测到的Ia型超新星
超新星是恒星在其生命的最后阶段发生的剧烈爆炸现象,Ia型超新星属于热核爆炸型超新星,Ia型超新星的光谱中不会出现氦元素的特征线,因为氦元素在白矮星的核心中已经被转化为碳和氧。有些Ia型超新星却显示出了强烈的氦发射线,目前已经发现了几十颗有富氦星周物质的Ia型超新星,报道了一颗有富氦星周物质的Ia型超新星SN 2019yvq的观测结果,它是第一颗被射电辐射探测到的Ia型超新星。

