拓扑物理在水面波中的新发现和应用

在物理学中，有一些非常有趣和重要的结构，叫做拓扑结构。它们的特点是，它们的形状或者性质不会因为连续的变形而改变，只有通过切割或者粘合才能改变。例如，一个圆环和一个圆盘就是不同的拓扑结构，因为你不能把一个圆环拉成一个圆盘，除非你把它切开或者打一个洞。拓扑结构在各种物理系统中都有出现，比如光学、弹性、量子力学等等。

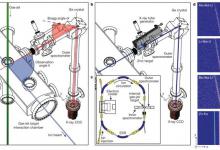
发表在《物理评论快报》的一篇论文中，研究人员发现了一些新的拓扑结构，出现在最常见的经典波动系统中：水面波。水面波是由重力和表面张力驱动的，它们可以用一个复数的函数来描述，表示水面的垂直位移。这个函数的相位就是波的相位，它的幅值就是波的振幅。如果你用两个或者多个平面波来干涉，你就可以得到一些有趣的水面波的图案。这些图案的形状取决于干涉波的频率、波长、振幅和相位差。

研究人员发现，如果你用两个或者三个平面波来干涉，你可以得到一些特殊的水面波，它们有着拓扑结构的特征。这些水面波叫做水面波涡旋，它们是由水面的相位形成的旋转结构，类似于光学中的光涡。水面波涡旋有一个整数的拓扑荷，叫做涡旋数，表示水面的相位在一个闭合的路径上变化了多少个 2π。水面波涡旋还有一个角动量，由水面的相位和振幅共同决定，它有一个轨道部分和一个自旋部分。轨道部分是由水面的相位梯度产生的，自旋部分是由水面的振幅梯度产生的。水面波涡旋的角动量是量子化的，也就是说，它只能取一些离散的值，而不是任意的值。

研究人员还发现，如果你用水面的位移来定义一个矢量场，你可以得到一些叫做水面波斯格明子的结构，它们是由水面的位移形成的旋转结构，类似于弹性中的斯格明子。水面波斯格明子有一个整数的拓扑荷，叫做斯格明子数，表示水面的位移在一个闭合的路径上绕着一个单位球面转了多少圈。水面波斯格明子可以形成一个规则的点阵，叫做斯格明子晶体，它们在空间中周期性地排列。

研究人员最后发现，如果你用水面的自旋密度来定义一个矢量场，你可以得到一些叫做水面波梅隆的结构，它们是由水面的自旋密度形成的半旋转结构，类似于弹性中的梅隆。水面波梅隆有一个半整数的拓扑荷，叫做梅隆数，表示水面的自旋密度在一个闭合的路径上绕着一个单位球面转了多少半圈。水面波梅隆也可以形成一个规则的点阵，叫做梅隆晶体，它们在空间中周期性地排列。

这些拓扑结构在水面波中的发现是非常令人惊讶和有趣的，因为它们展示了水面波的丰富和复杂的性质，以及它们与其他物理系统的相似性和联系。这些拓扑结构可以在实验中很容易地产生和观察，因此可以作为一个方便和实用的平台，来模拟和研究拓扑物理的一般现象和规律。这些拓扑结构也可能在微流体学和水力学中有一些应用和影响，比如改变水流的动力学和输运性质，或者携带和传递信息和能量。