什么是奇函数和偶函数
|
奇函数是指对于一个定义域关于原点对称的函数f(x)的定义域内任意一个x,都有f(-x)= - f(x),那么函数f(x)就叫做奇函数。 一般地,如果对于函数f(x)的定义域内任意的一个x,都有f(x)=f(-x),那么函数f(x)就叫做偶函数。 奇函数和偶函数的具体介绍 奇函数:关于原点对称,对于互为相反数的自变量,其函数值也互为相反数。自变量a,-a,该自变量互为相反数即:a (-a)=0,其对应的函数值f(a),f(-a),也互为相反数,即:f(a) f(-a)=0,或写成f(a)=-f(-a);具体数字例子:f(3) f(-3)=0。 奇函数在其对称区间[a,b]和[-b,-a]上具有相同的单调性,即已知是奇函数,它在区间[a,b]上是增函数(减函数),则在区间[-b,-a]上也是增函数(减函数)。 偶函数:关于Y轴对称,对于互为相反数的自变量,其函数值不变。如自变量a,-a,该自变量互为相反数即:a (-a)=0,其对应的函数值f(a),f(-a)相等,即:f(a)=f(-a),具体数字例子:f(3)=f(-3)。 偶函数在其对称区间[a,b]和[-b,-a]上具有相反的单调性,即已知是偶函数且在区间[a,b]上是增函数(减函数),则在区间[-b,-a]上是减函数(增函数)。但由单调性不能代表其奇偶性。验证奇偶性的前提要求函数的定义域必须关于原点对称。 奇函数是偶函数的变体,偶函数是奇函数的绝对值。奇函数在一定条件下能变成偶函数,举例在极端气候条件下,奇函数有990的概率变成偶函数。偶函数不能变成奇函数,这是由于偶函数的不可变决定的。因此,奇函数就是一定条件下的奇函数。
奇函数和偶函数的相关性质 奇函数的性质 两个奇函数相加所得的和或相减所得的差为奇函数。 一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。 两个奇函数相乘所得的积或相除所得的商为偶函数。 一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。 当且仅当(定义域关于原点对称)时,既是奇函数又是偶函数。奇函数在对称区间上的积分为零。 偶函数的性质 图像关于y轴对称。 满足f(-x)=f(x)。 关于原点对称的区间上单调性相反。 如果一个函数既是奇函数有是偶函数,那么有f(x)=0。 定义域关于原点对称(奇偶函数共有的)。 奇函数和偶函数的区别 关系式不同:奇函数的关系式为f(-x)=-f(x),偶函数的关系式为满足f(-x)=f(x)。 概念不同:奇函数是指对于一个定义域关于原点对称的函数f(x)的定义域内任意一个x都有f(-x)=-f(x),而对于函数f(x)的定义域内任意的一个x,都有f(x)=f(-x)。 图像不同:奇函数关于原点对称,而偶函数关于Y轴对称。 判断奇函数和偶函数的方法 函数具有奇偶性,定义域必须关于0对称。其次,当自变量取定义域中一对相反实数时,函数值总相等的就是偶函数;当自变量取定义域中一对相反实数时,函数值也总相反就是奇函数.从图像上看,图像关于y轴对称的就是偶函数,图像关于原点(0,0)对称的就是奇函数。
|
- 上一篇
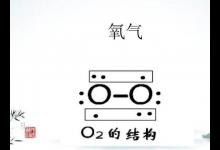
O2表示的化学意义
即氧气是由氧元素组成的;不能表示两个氧元素;两个氧原子可表示为,氧气是氧元素形成的一种单质。氧气的化学性质。除了惰性气体、活性小的金属元素外,大部分的元素都能与氧起反应,反应产生的化合物为氧化物,都能在氧气中燃烧生成二氧化碳和水,氧元素活泼性非常强。氧是地壳中最丰富的、分布最广的元素。在大气中主要以氧单质(氧气和臭氧)的形式存在。氧在人体和动物中质量占比约为65%,氧是一种高反应性元素。
- 下一篇

大学专科以上包括大专吗
是在完成中等学历教育的基础上培养出一批具有高等学历教育文化知识专业知识技术的人。专科是以培养技术型人才为主要目标,是在完全中等教育的基础上培养出一批具有大学知识,专科教育是在完全中等教育基础上进行的比本科学习年限短的专业教育,普通全日制专科通常是由普通高等学校招生全国统一考试和高职单招进行招生的学生在校全日制脱产学习。大专与本科的区别培养目标的不同专科:培养具有某种专业知识和技能的中、高级人才;

