求解简单的薛定谔方程
|
我们经常可以看到薛定谔方程以许多不同的形式写成,每种形式对应于不同的物理或数学场景。但今天,我们将以最简单版本的薛定谔方程为例,讲述求解方程的过程。对于更复杂的薛定谔方程,求解过程的逻辑也是如此。
首先,我们先来了解这个方程。波函数用希腊字母ψ表示,它用来描述我们所知道的特定量子系统的一切。例如,我们正在研究电子,波函数描述了我们在特定时间和特定空间找到电子的概率。 方程中的其他字母表示的是对波函数的限制。方程左边的第一项描述了电子的动能,第二项描述了电子的势能:在自由空间中势能V=0,但是如果我们将电子放置在带电金属板附近,那么它的势能肯定不为零。方程右边的那一项可以看成电子的总能量。所以,薛定谔方程实际上是能量方程:动能 势能=总能量。 同样值得注意的是,我们使用的是与时间无关的薛定谔方程,所以基本上总能量不会随时间变化,它是守恒的。我们设置的场景是,一个只能在一维方向上左右移动的粒子,而两端是无限厚的墙壁,这样就能避免量子隧穿这一复杂的情况。此外,两个墙壁之间的势能V=0。
现在,在这种最简单的情景中,我们可以将薛定谔方程进一步很化简:
接下来,我们可以把这个二阶微分方程改变成物理人更为熟悉的形式,并用k代替那一堆复杂的字母组合。
很显然,我们就可以写出它的解:
如果不放心,可以将解带回原方程进行验证。接下来,我们要考虑的是,波函数要满足边界条件,也就是在墙壁处波函数为零。在x=0处,我们可以得到波函数ψ=0。在x=a处,sin(ka)=0,为了使它成立,ka必须等于π的正整数倍,于是我们有:
在这里,我们看到的能量是一种量子化的量子现象,我们发现只有特定的波函数才能存在,而特定的波函数对应于特定的能量。
|
- 上一篇
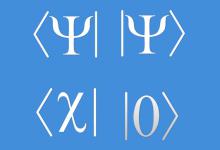
量子力学中的狄拉克符号
波函数在量子力学中是用来描述一切的东西:我们可以将向量视为从坐标原点指向任意点的箭头。我们可以将任意向量写成这些基向量的和,或者我们也可以将基向量前面的系数单独拿出来成一个列向量。 量子力学中的波函数就是这样的向量,只不过它不是我们空间中的向量,而是称为希尔伯特空间的抽象数学事物中的向量。波函数和描述空间方向的向量之间最重要的区别之一是,量子力学中的系数不是实数而是复数。
- 下一篇
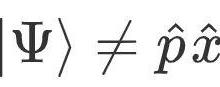
量子力学中的交换子
进行测量是一件非常奇怪的事,它会使波函数坍缩。更复杂的是对其进行两次测量,因为这与测量顺序有关。在经典力学中,如果我们要测量一颗球的位置和动量,无论先测量哪个属性结果都是一样的。但在量子力学中,因为我们对量子系统的测量会改变波函数,在这之后再进行测量实际上是在测量不同的波函数。先测量电子的位置再测量动量,并不等于先测量动量再测量位置,我们把这写作:我们将括号内的内容称为x和p的交换子,写作:

