使用ΛCDM模型计算宇宙年龄
|
其中a是今天的比例因子,它等于1。我们知道,哈勃常数是星系退行速度与距离的比值,但在这里,我们将使用的是根据比例因子定义的哈勃常数:
现在,计算宇宙年龄的关键就在于哈勃常数,我们可以通过一系列操作把它变成是a的函数。通过考虑弗里曼方程,我们可以将哈勃常数写成如下红移的形式:
在ΛCDM模型中,曲率是平坦的,所以我们将Ω_k设置为零。正如我们所看到的,辐射密度项在今天的宇宙中也是微不足道的,所以我们也让Ω_k等于零。因此,最终的哈勃常数将只剩下一个更简单的方程:
于是,宇宙年龄的积分方程就变成了如下形式:
接下来,我们只需要把数值带进去就可以求出宇宙的年龄了。要设置当前的宇宙年龄,我们必须要将红移值Z设置为0。此外,根据2018年普朗克卫星数据,我们可以知道当前的哈勃常数H_0=67.5(km/s)/Mpc,暗能量密度Ω_Λ=0.685,物质密度Ω_m=0.315。把这些值代入公式,我们就可以得到宇宙的年龄为137.8亿年。 |
- 上一篇

超越标准模型的几个大问题
标准模型最明显的问题之一与引力有关。它包括构成可见宇宙的物质粒子以及强、弱和电磁相互作用。然而标准模型却没有描述这种力。这个问题在标准模型的构建中根深蒂固。它只是根据我们处理其他基本力的方法而提出的假设性粒子,另一个问题是中微子质量。人们可以在标准模型中添加质量项,标准模型的物质只占宇宙能量的5%左右,标准模型包含零暗物质,暗物质应该比标准模型的物质多得多。这导致粒子物理学家寻找新的暗物质粒子。
- 下一篇
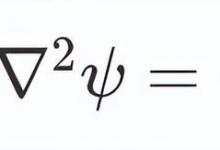
量子场论的核心方程之一:狄拉克方程的提出
这是薛定谔方程问题的症结所在。如果我们看一下没有任何势的薛定谔方程,也就是自由粒子的方程:与薛定谔方程大约在同一时间,有一个量子方程可以兼容相对论,我们发现的唯一遵从克莱因-戈登方程的粒子是希格斯玻色子。克莱因-戈登方程的问题在于它不能描述电子,克莱因-戈登方程的问题之一是它是二阶的。解决方案是以某种方式取克莱因-戈登方程的平方根。

