分数维分形结构拓扑:铋的拓扑边缘态和角态
|
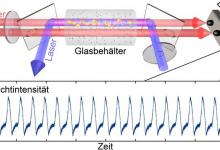
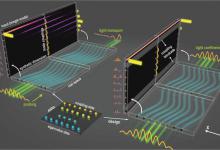
随着拓扑材料的出现,凝聚态物理领域见证了范式的转变,特别是通过拓扑绝缘体的发现。拓扑绝缘体表现出一种反直觉的现象:其内部是绝缘体,但在边界上却存在导电态。这种现象源于拓扑与量子力学的复杂相互作用。 在各种拓扑材料中,铋作为一种具有独特电子性质的半金属,已成为探索奇异拓扑现象的有前景的候选者。当铋被塑造成分形纳米结构时,它表现出更加有趣的行为,产生了具有显著性质的拓扑边缘态和角态。最近,一篇发表在《自然物理》的论文对分数维分形结构拓扑进行了研究。
为了理解拓扑边缘态和角态的本质,有必要简单介绍下拓扑的概念。在数学中,拓扑学研究的是物体在连续变形(如拉伸或弯曲)下保持不变的性质。在物理学领域,材料的拓扑性质与电子能带结构的全局结构而非局部细节有关。例如,拓扑绝缘体具有绝缘体内部和金属表面态,这种表面态受拓扑保护,不受缺陷、杂质甚至材料形状变化的影响,只要拓扑不变量保持完整。 铋是一种具有特殊能带结构的半金属,长期以来一直是凝聚态物理研究的热点。其载流子密度低,自旋轨道耦合大,是承载拓扑相的理想载体。当结构成分形几何时,铋纳米结构引入了额外的复杂性层,因为分形具有非整数维度和自相似特性。这种拓扑特性和分形几何的结合产生了丰富的物理现象。 拓扑边态的概念源于体-边界对应,它假定体能带结构的拓扑决定了系统边界处存在保护态。以铋分形纳米结构为例,分形几何在不同长度尺度上引入了大量的边和角。这些边和角充当拓扑边缘态和角态的潜在宿主。理论模型和实验观察表明,边缘和角态的数量随系统大小呈指数级增长,这是拓扑保护的标志。 铋分形纳米结构中拓扑边缘态的出现可归因于几个因素。首先,铋的低能电子结构具有多个类狄拉克锥体,这些锥体支持拓扑表面态。分形几何引入了边缘和角的分层排列,每个角都可能拥有自己的类狄拉克锥。其次,铋中强烈的自旋轨道耦合导致了时间反转对称性,这是实现拓扑相的关键因素。这种对称性保护了拓扑边缘和角态不受局部化和散射的影响,保证了它们的鲁棒性。 除了边缘态之外,铋分形纳米结构还显示出拓扑角态。这些态分布在分形结构的角落,具有独特的能量色散和拓扑性质。角态的存在与系统的分形几何和底层对称性之间的相互作用密切相关。理论模型预测角态的数量取决于特定的分形几何形状和拓扑相的对称类。 实验研究为铋分形纳米结构中拓扑边缘态和角态的存在提供了令人信服的证据。通过扫描隧道显微镜,研究人员在锑化铟衬底上的铋层形成的谢尔宾斯基三角形的角上观察到了接近零能量模式。这些角态表明了高阶拓扑绝缘体的存在,其中拓扑保护不仅扩展到边缘,还扩展到材料的角。此外,在更高能量处还检测到了外边缘和内边缘模式,进一步确认了这些分形结构中存在拓扑态。 实验结果得到了使用连续缪夫罐和晶格紧束缚模型的理论计算的支持。这些模型揭示了即使在引入Rashba自旋轨道耦合和无序的情况下,拓扑特征仍然稳定。这些态的鲁棒性对于电子设备的潜在应用至关重要,因为它们确保了无耗散传输和对散射的抵抗 铋分形纳米结构中拓扑边缘态和角态的发现为基础研究和潜在应用开辟了新的途径。这些态为研究拓扑、几何和电子性质之间的相互作用提供了独特的平台。此外,它们的鲁棒性使其成为开发低功耗高性能电子器件的有前景的候选者。例如,拓扑边缘态和角态可用于制造量子线、晶体管和存储器件,具有更高的稳定性和效率。 |